
Eux dont la présence était si bruyante, ils sont partis sans un bruit et depuis le jardin est silencieux.
Peut-être un de ceux qui sont nés ici se souviendront de l'endroit l'année prochaine quand ils voudront devenir parents à leur tour.
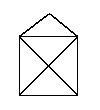
Le retour de la théorie des graphes :
Certains d'entre nous se sont amusés, enfants, à chercher comment dessiner cette petite maison sans soulever le crayon de la feuille et sans repasser 2 fois sur un même trait.
Pendant un cours soporifique par exemple. Peut-être même un cours de maths.
Et bien nous faisions des maths sans le savoir.
Transformons la petite maison en graphe : 4 sommets, 7 arêtes
2 sommets pairs, 2 sommets impairs

On a déjà vu qu'il n'était pas possible de trouver un circuit fermé, mais si on ne s'oblige pas à revenir au point de départ ?
C'est encore Euler qui fournit la réponse.
Si un graphe ne possède pas plus de 2 sommets impairs, c'est bon, on peut parcourir le graphe, sans repasser sur une arête et sans lever le crayon.
Si on a compris le raisonnement expliqué pour les ponts de P. et tirouquin en promenade, on comprend sans trop de mal pourquoi un sommet impair ne peut être que point de départ ou d'arrivée du chemin, et donc pourquoi à partir de 3 sommets impairs ce n'est plus possible.
Ainsi donc la petite maison peut être dessinée d'un seul geste mais en partant ou arrivant des sommets 1 et 4, par exemple 1-2-3-1-4-2-3-4.

Grâce à Euler on peut donc savoir avant d'essayer s'il est possible de dessiner cette fleur sans lever le crayon et s'il faut partir et arriver de points particuliers.
A votre avis ?

11 commentaires:
PREM'S !!!!!
on peut la tracer et il faut partir de la queue, seul sommet impair de la fleur. J'ai bon dis, j'ai bon ??? j'ai mon bac ???? j'ai gagné quoi ??
euh si je m'ai plantée t'es gentil t'efface mon comm hein ;-)) j'ai une réputation à sauvegarder ! mdr !
deuzzzz...
au fait... c'est bien tu as bien retenu ma leçon sur la cravate et trouvé papa et maman mésange, je suis très fière de toi ;-) pas de trace de la famille mésange par chez moi par contre, désolée... j'ai des merles, des pigeons, des moineaux, des mésanges charbonnières mais pas de mésanges bleues...
ben... pour la pititmaison, ya pas 5 sommets par hasard non ? la pointe du toit n'est pas considérée comme un sommet ?
bon, sinon la fleur on peut la dessiner aussi en partant du haut de la tige (commencer par les pétales, puis le rond du centre, et descendre la tige)
mais je le sais juste paske j'ai essayé dans les 2 sens... pas paske j'aurais compris Euler, hein... (moi aussi je dois tenir ma réputation, hihihi)
Pareil, j'y arrive... Soit en partant du bas de la tige, soit du haut (comme Dodinette). Mais je suis proprement infoutue de voir si les feuilles ou les pétales sont des sommets impairs ou quelque chose d'approchant... Bref, capable de pratiquer, mais incapable de théoriser, quoi (comme souvent)
lily, tu as juste oublié le point où la tige rencontre la fleur, c'est également un sommet impair. On peut en effet la dessiner, en partant de l'une des extrémités de la tige et en arrivant à l'autre, comme anitta et dodinette l'ont vu également.
dodinette, pour la maison, tu peux considérer la pointe du toit comme un sommet... ou pas.
anitta, c'est pourtant simple, on regarde les points où arrivent plusieurs lignes, et on compte le nombre de lignes. (on considère aussi comme sommets les départs de ligne)
Ah si on m'avair expliqué les maths comme toi, j'aurais eu un bac C et non A ;-)
(avec pourtant auparavant 2 secondes C et une première D !)
Madeleine, il n'est jamais trop tard (sauf que ça s'appelle S maintenant mais c'est pas grave)
bon et alors y en a conbien des sommets dans cette fleur ( que j'arrive à dessiner, mais à pas à Ha sommer
zoé, on peut en compter 11 de sommets, dont seulement 2 impairs.
Sympa cette note.
merci, beverycool
(c'est ma seconde note sur les graphes, j'ai commencé par les classiques ponts quelques notes avant celle-ci)
Enregistrer un commentaire